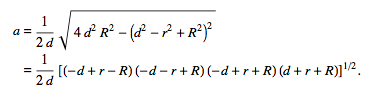Notes:Inverse kinematics Revision as of 21:12, 20 April 2018 by Frankiezafe (Talk | contribs)
Notes about computation of inverse kinematics[1], first implementation done in threejs[2].
Spheres
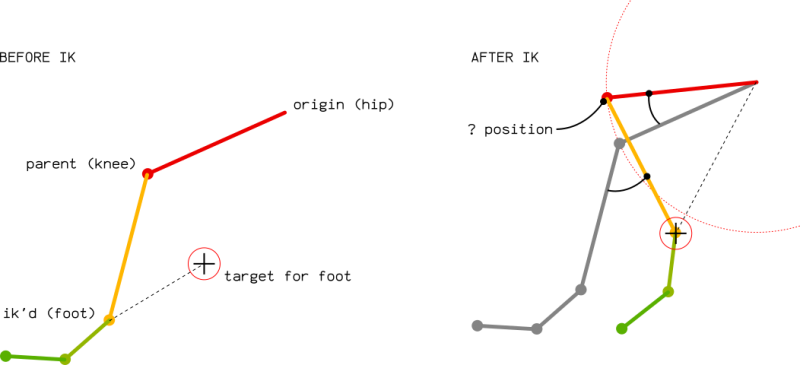
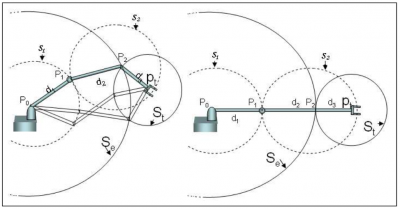
At this moment, the research is focusing on solving a 2 bones system, the leg in this case, but it would be applicable on the arms or any other part of a skeleton having at least 2 parents.
The main issue seems to be the computation of the knee position. All distances are easily computed:
- upperleg (red) keeps its length
- leg (yellow) keeps its length also
- distance between the target and the origin of the upper leg can be easily computed in world space.
Rendering the position of the knee is crucial to compute the rotation of the upper leg. Once correct, the rotation of the leg will be simple to render, as it is the rotation from the current direction to the [knee - target] direction.
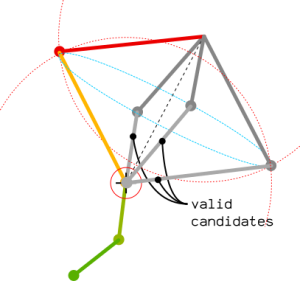
A little warning: the graphic here above is in 2d. In a 3d world, the position of the knee is a circle on a sphere: any point being at the right distance of the target point and the upperleg origin will be a valid candidate! The circle of possibilities is the intersection of 2 spheres having their radii equals to bones length.
The radius of the cyan circle can be solved by using this equation[3]:
a = 1/(2d)sqrt(4d^2R^2-(d^2-r^2+R^2)^2)
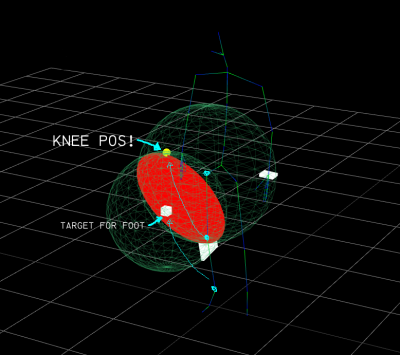
A little screenshot for better readability:
The tricky point is to forget about the spheres' position and only consider the distance of their centers as the d parameter. The normal of the intersection plane can be computed independently.
Implementation of the equation in an openprocessing sketch.
Selecting a point on the circle
To select a point on the intersection of the 2 spheres, I first computed a quaternion representing the rotation to apply on a unit vector. As the Z axis is pointing forward in the model i've used, I used a vector( 0, 0, 1 ) to compute the orientation:
var spheres_center_quat = new THREE.Quaternion().setFromUnitVectors( new THREE.Vector3( 0, 0, 1 ), spheres_center_dir.clone().normalize() );
I apply this orientation on a perpendicular vector, vector( 0, 1, 0 ) and multiply it by the circle's radius (CRAD).
We now have the offset relatively to the circle center, but we still don't know where it is. Basic geometry will give us its location:
var length = Math.sqrt( Math.pow( sphereA_radius,2 ) - Math.pow( CRAD,2 ) );
The circle's center position is found by adding the normalised vector joining the 2 spheres centers, multiplied it by this length, to the position of the sphereA.
The target position is found by adding the offset to the circle's center, represented here below by the yellow sphere.
End of the day, computation of knee position is correct, none of the two vectors above have been used.
References
- ↑ Inverse kinematics sur wikipedia
- ↑ Three.js is a 3d rendering engine written in javascript, more on wikipedia
- ↑ Sphere-Sphere Intersection
- Animation Bootcamp: An Indie Approach to Procedural Animation - a GDC talk about character animation in a computation effective way.
- Inverse kinematics on roblox via Sébastien Courvoisier.
- Inverse kinematics computation in computer graphics and robotics using conformal geometric algebra by Dietmar Hildenbrand, Julio Zamora and Eduardo Bayro-Corrochano, AMS Subject Classification: 15A66, 17B37, 20C30, 81R25 pdf.