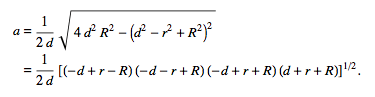Difference between revisions of "Notes:Inverse kinematics"

Revision as of 08:48, 23 April 2018

Notes about computation of inverse kinematics^[1], first implementation done in threejs^[2].

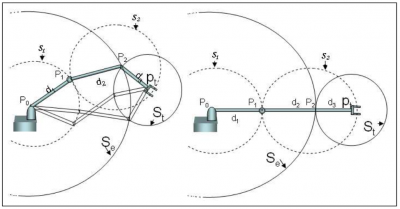
At this moment, the research is focusing on solving a 2 bones system, the leg in this case, but it would be applicable on the arms or any other part of a skeleton having at least 2 parents.

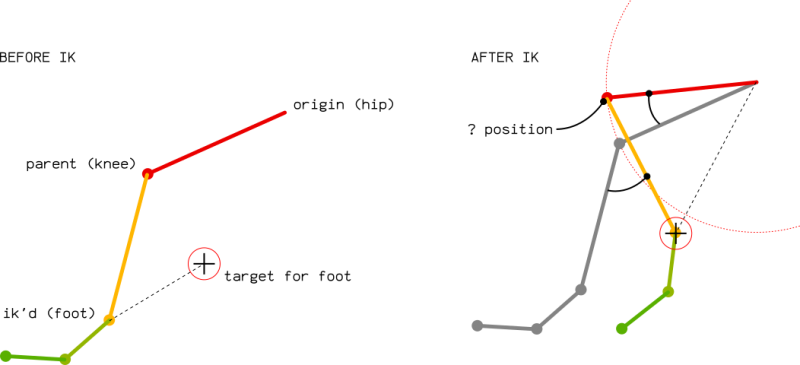
The main issue seems to be the computation of the knee position. All distances are easily computed:

• upperleg (red) keeps its length
• leg (yellow) keeps its length also
• distance between the target and the origin of the upper leg can be easily computed in world space.

Rendering the position of the knee is crucial to compute the rotation of the upper leg. Once correct, the rotation of the leg will be simple to render, as it is the rotation from the current direction to the [knee - target] direction.

Spheres

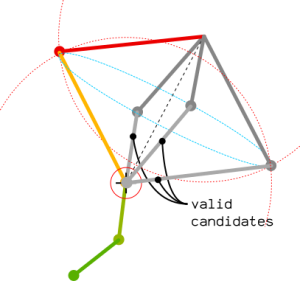
A little warning: the graphic here above is in 2d. In a 3d world, the position of the knee is a circle on a sphere: any point being at the right distance of the target point and the upperleg origin will be a valid candidate! The circle of possibilities is the intersection of 2 spheres having their radii equals to bones length.

The radius of the cyan circle can be solved by using this equation^[3]:

a = 1/(2d)sqrt(4d^2R^2-(d^2-r^2+R^2)^2) 

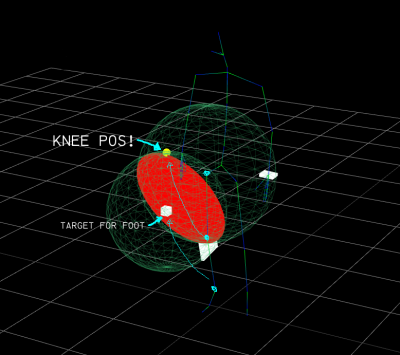
A little screenshot for better readability:

The tricky point is to forget about the spheres' position and only consider the distance of their centers as the d parameter. The normal of the intersection plane can be computed independently.

Implementation of the equation in an openprocessing sketch.

Selecting a point on the circle

To select a point on the intersection of the 2 spheres, we first computed a quaternion representing the rotation to apply on a unit vector. As the Z axis is pointing forward in the model, we can use a vector( 0, 0, 1 ) to compute the orientation:

var spheres_center_quat = new THREE.Quaternion().setFromUnitVectors( 
			new THREE.Vector3( 0, 0, 1 ), 
			spheres_center_dir.clone().normalize() );

We apply this rotation on a perpendicular vector, vector( 0, 1, 0 ) in this case, and multiply it by the circle's radius (CRAD).

var offset = new THREE.Vector3( 0, 1, 0 );
offset.applyQuaternion( spheres_center_quat );
offset.multiplyScalar( CRAD );

We now have the offset relatively to the circle center, but we still don't know where it is. Basic geometry will give us its location:

var length = Math.sqrt( Math.pow( sphereA_radius,2 ) - Math.pow( CRAD,2 ) );

The circle's center position is found by adding the normalised vector joining the 2 spheres centers multiplied by this length, to the position of the sphereA.

The knee position is found by adding the offset to the circle's center, represented here below by the yellow sphere.

End of the day, computation of knee position is correct, none of the two vectors above have been used.

Bone's rotation

Solving the rotation of the bones is trickier than it seems. This is due to the fact that the circle of sphere's intersection gives an infinity of valid positions. It is easy for a human to point the right position on this circle (the knee / elbow should be there). The second step of the algorithm has been to identify a good procedure to find a plausible point.

References

1. ↑ Inverse kinematics sur wikipedia
2. ↑ Three.js is a 3d rendering engine written in javascript, more on wikipedia
3. ↑ Sphere-Sphere Intersection

• Animation Bootcamp: An Indie Approach to Procedural Animation - a GDC talk about character animation in a computation effective way.
• Inverse kinematics on roblox via Sébastien Courvoisier.
• Inverse kinematics computation in computer graphics and robotics using conformal geometric algebra by Dietmar Hildenbrand, Julio Zamora and Eduardo Bayro-Corrochano, AMS Subject Classification: 15A66, 17B37, 20C30, 81R25 pdf.

• Frenet–Serret formulas, about normals and tangents.

• How to project a point onto a plane in 3D? on stackoverflow.