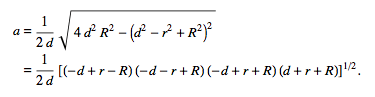Difference between revisions of "Notes:Inverse kinematics"
Frankiezafe (Talk | contribs) |
Frankiezafe (Talk | contribs) |
||
| Line 7: | Line 7: | ||
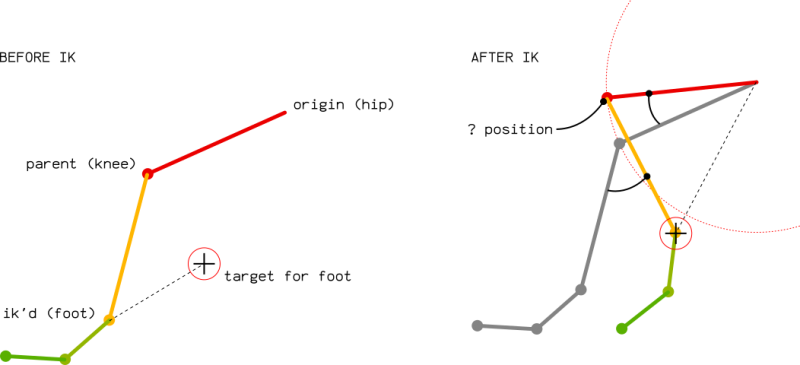
The main issue seems to be the computation of the knee position. All distances are easily computed: | The main issue seems to be the computation of the knee position. All distances are easily computed: | ||
| − | * | + | * upperleg (red) keeps its length |
* leg (yellow) keeps its length also | * leg (yellow) keeps its length also | ||
* distance between the target and the origin of the upper leg can be easily computed in world space. | * distance between the target and the origin of the upper leg can be easily computed in world space. | ||
| − | Rendering the position of the knee is crucial to compute the rotation | + | Rendering the position of the knee is crucial to compute the rotation of the upper leg. Once correct, the rotation of the leg will be simple to render, as it is the rotation from the current direction to the [knee - target] direction. |
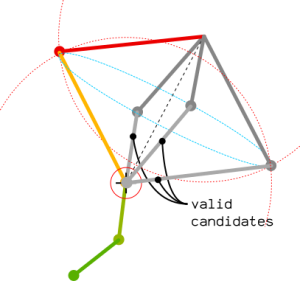
A little warning: the graphic here above is in 2d. In a 3d world, the position of the knee is a circle on a sphere: any point being at the right distance of the target point '''and''' the upperleg origin will be a valid candidate! The circle of possibilities is the intersection of 2 spheres having their radii equals to bones length. | A little warning: the graphic here above is in 2d. In a 3d world, the position of the knee is a circle on a sphere: any point being at the right distance of the target point '''and''' the upperleg origin will be a valid candidate! The circle of possibilities is the intersection of 2 spheres having their radii equals to bones length. | ||
| Line 25: | Line 25: | ||
[[File:Sphere-Sphere Intersection.png]] | [[File:Sphere-Sphere Intersection.png]] | ||
| − | The tricky point is to forget about the spheres | + | The tricky point is to forget about the spheres' position and only consider the distance of their centers as the ''d'' parameter. The normal of the intersection plane can be computed independently. |
<html><iframe src="https://www.openprocessing.org/sketch/539606/embed/?plusEmbedHash=ZTk4N2UyMzUyM2U4ZDc5OWUzYmYyM2NkYjZjYTUwNGYyZGU0YTNhMjJlZDM0NTI2NzE2NzlmMzM4MThmZTRkNTU1NjFiOGU1ZjhjYThmNGJhMTlkYTgxNmJhZjJkM2NmYjI3OTBlNDBlNzBhYjNlZjFiNmI5NDg3MGRkMDYyOWYwU2ZqdDEvS2ZaMHJiaUtKeWY3WkJXVDRYQ1J1bUpBUXYzZklmSnRBTjQrU1Fid3NMbzhxSWlsbUU4Q0ZKT1dEQ1luRjZoVmVxY1FGcnZNR2g1dnBiZz09" width="800" height="600"></iframe></html> | <html><iframe src="https://www.openprocessing.org/sketch/539606/embed/?plusEmbedHash=ZTk4N2UyMzUyM2U4ZDc5OWUzYmYyM2NkYjZjYTUwNGYyZGU0YTNhMjJlZDM0NTI2NzE2NzlmMzM4MThmZTRkNTU1NjFiOGU1ZjhjYThmNGJhMTlkYTgxNmJhZjJkM2NmYjI3OTBlNDBlNzBhYjNlZjFiNmI5NDg3MGRkMDYyOWYwU2ZqdDEvS2ZaMHJiaUtKeWY3WkJXVDRYQ1J1bUpBUXYzZklmSnRBTjQrU1Fid3NMbzhxSWlsbUU4Q0ZKT1dEQ1luRjZoVmVxY1FGcnZNR2g1dnBiZz09" width="800" height="600"></iframe></html> | ||
Revision as of 17:04, 19 April 2018
Notes about computation of inverse kinematics[1], first implementation done in threejs[2].
At this moment, the research is focusing on solving a 2 bones system, the leg in this case, but it would be applicable on the arms or any other part of a skeleton having at least 2 parents.
The main issue seems to be the computation of the knee position. All distances are easily computed:
- upperleg (red) keeps its length
- leg (yellow) keeps its length also
- distance between the target and the origin of the upper leg can be easily computed in world space.
Rendering the position of the knee is crucial to compute the rotation of the upper leg. Once correct, the rotation of the leg will be simple to render, as it is the rotation from the current direction to the [knee - target] direction.
A little warning: the graphic here above is in 2d. In a 3d world, the position of the knee is a circle on a sphere: any point being at the right distance of the target point and the upperleg origin will be a valid candidate! The circle of possibilities is the intersection of 2 spheres having their radii equals to bones length.
The radius of the cyan circle can be solved by using this equation[3]:
a = 1/(2d)sqrt(4d^2R^2-(d^2-r^2+R^2)^2)
A little screenshot for better readability:
The tricky point is to forget about the spheres' position and only consider the distance of their centers as the d parameter. The normal of the intersection plane can be computed independently.
Implementation of the equation in an openprocessing sketch.
We need to pick a point on this circle by using an arbitrary direction:
- front axis of the leg or
- knee - target difference.
References
- Animation Bootcamp: An Indie Approach to Procedural Animation - a GDC talk about character animation in a computation effective way.