WorkUnit:Disrupted Cities - road network Revision as of 19:05, 21 April 2017 by Frankiezafe (Talk | contribs) (diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)

This page describes the different steps implemented in the city generator package to detect block in the road's network, in a fast and clean way.

sketches

These sketches cover the whole research described below. They are displayed chronologically.

block detection

right vector

• 
• 
• 
• 
• 

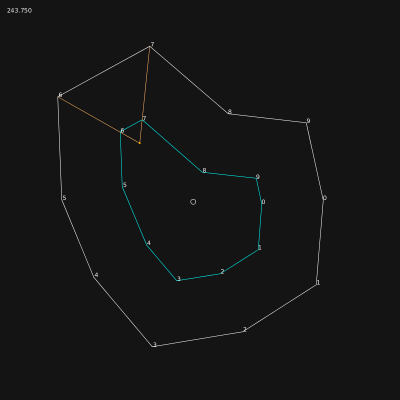
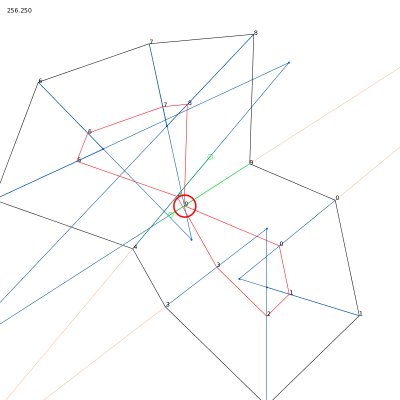
Finding the closest road on the right at a crossroad.

To generate the bocks of building based on the roads structure, the method I’m building is based on a simple idea: when you arrives at a crossroad, you take the first street on the right and you go on like this until you reach a dead-end or your starting point. If you reach your starting point, the succession of roads you took defines a block of building. In theory. This technique has been suggested by Michel Cleempoel, on the way back from school.

After a bit of preparation of the road network (removing orphan roads, having no connection with others, and dead-ends parts of the roads), the real problem arouse: how do you define right in a 3d environment, without an absolute ground reference. Indeed, I can configure the generator to use the Y axis (top axis in ogre3d) in addition to X & Z.

At a crossroad, you may have several possibilities of roads. In the research, these possible roads are reduced to 3d vectors, all starting at world’s origin. The goal is to find the closest vector on the right of the current one, called the main 3d vector in the graphic above..

The right is a complex idea, because it induces an idea of rotation. The closest on the right doesn’t mean the most perpendicular road on the right side. Let say I have 4 roads to choose from. Two going nearly in the opposite direction of the road i’m on, one perpendicular and one going straight on.

If I compute the angles these roads have with the current one, results are:

• 5°,
• -5°,
• 90°,
• and 170°.

The winner is not the 90°, but the 5° road! If I sort them, the last one must be the -5°, who is the first on the left.

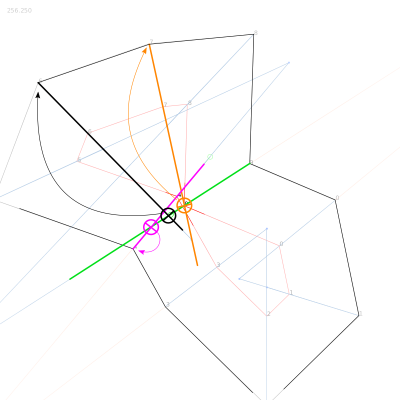
3d plane from a 3d vector

The first thing to do is to define reference plane. To do so, you get the normal vector of the road by doing a cross product with the UP axis (Y axis in this case). The normal gives you a second vector, perpendicular to the road, and therefore defines a plane. Let’s call it VT plane, for Vector-Normal plane. For calculation, we need the vector perpendicular to this plane, rendered by crossing the road and its normal, let’s call it the tangent vector. Until here, it’s basic 3d geometry.

projection of 3d vectors on a plane

We can now project all the possible roads on the VT plane. These are the yellow vectors in the graphic. The math are clearly explained by tmpearce. Once implemented, it looks like this:

float d = othervector.dot( tangent );
vec3f projectedvector;
projectedvector += tangent;
projectedvector *= d * -1;
projectedvector += othervector;

We are nearly done!

angle between 3d vectors

The projected vectors will help the angle calculation. Indeed, the current vector and the projected ones being coplanar, they share the same normal. The way to get the angle between 2 coplanar vectors is described by Dr. Martin von Gagern, once again. See Plane embedded in 3D paragraph for the code i’ve used.

And… tadaaammmm! The number rendered by the method is the angle i was searching for, displayed in degrees in the graphic above.

The c++ implementation of the method is looking like this:

RDListIter it;
RDListIter ite;

vec3f dir = ( *from )-( *this );
vec3f normal = GLOBAL_UP_AXIS.getCrossed( dir );
normal.normalize( );
vec3f tangent = dir.getCrossed( normal );
tangent.normalize( );

it = connected_dots.begin( );
ite = connected_dots.end( );

RoadDot* sel_dot = 0;
float smallest_angle = -1;

for (; it != ite; ++it ) {

    if ( (*it) == from ) {
         continue;
    }

    vec3f nv = ( *( *it ) )-( *this );
    nv.normalize( );

    // http://stackoverflow.com/questions/9605556/how-to-project-a-3d-point-to-a-3d-plane#9605695
    float d = nv.dot( tangent );
    vec3f nn = nv + tangent * d * -1;

    // http://stackoverflow.com/questions/14066933/direct-way-of-computing-clockwise-angle-between-2-vectors
    float dot = nn.x * dir.x + nn.y * dir.y + nn.z * dir.z;
    float det =
              nn.x * dir.y * tangent.z +
              dir.x * tangent.y * nn.z +
              tangent.x * nn.y * dir.z -
              nn.z * dir.y * tangent.x -
              dir.z * tangent.y * nn.x -
              tangent.z * nn.y * dir.x;

    float angle = atan2( det, dot );

    if ( angle < 0 ) { 
         angle += TWO_PI;
    }

    if ( sel_dot == 0 || smallest_angle > angle ) {
         sel_dot = ( *it );
         smallest_angle = angle;
    }

}

return sel_dot;

• RDListIter is a typedef vector<RoadDot*>
• GLOBAL_UP_AXIS allows to define wich is the UP axis of the world.
• vec3f is a standard class for 3d vector manipulation, depending on your framework.

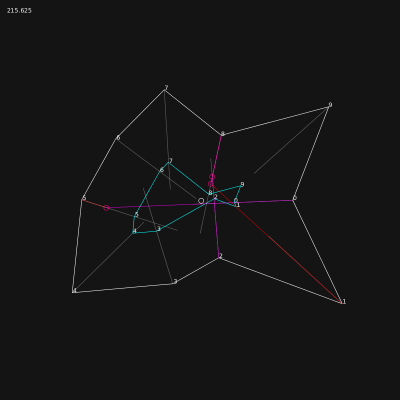
half-edges

See method chapter for a resume of the implementation.

Isle::collect_oriented_segments(Road* r)

cases to foresee:
0. starting the road, previous dot has one connection
1. starting the road, previous dot has >1 connections > crossroad
2. along the road, current dot has two connections 
3. along the road, current dot has >2 connections > crossroad
4. end of the road, current dot has one connection
5. end of the road, current dot has >1 connections > crossroad

A       B       C
o ----> o ----> o
        ^
        |
        |
        D

[f]  [f]  [b]  [b]  [f]
AB > BC > CB > BA > AB

[f]  [b]  [f]  [f]  [b]  [b]  [f]
AB > BD > DB > BC > CB > BA > AB


A       B       C
o ----> o ----> o
        |
        |
        v
        D

[f]  [f]  [b]  [f]  [b]  [b]  [f]
AB > BD > DB > BC > CB > BA > AB

cases [2,5] can happens simultaneously

It seems nearly impossible to create the relation between half-edges correctly in one pass: some half-edges tries to connect to not yet created half-edges. If the half-edges are generated on the fly, it will imply a check at each half-edge (HE) generation, to validate if the HE is already created or not.

A better approach seems to be: generation of all of them + creation of structures for crossroads, holding a pointer to the RoadDot and the list of all HEs connected to it. Connections can be resolved locally in a second pass. Let's try it.

Not yet functional: blocks are crossing roads...

The issue was coming from a method that sort the connections of a roaddot: RoadDot::rightSort(RDList& sorted). In its first implementation, I was just looping over the connections and storing in a list the result of the method RoadDot::getRight(RoadDot* from);, without checking in any way the angles between these dots. The block crossing street issue was caused by this inconsistency. I now use a skip list and I always use the first connection as a reference. Code is simple:

void RoadDot::rightSort( RDList& sorted ) {
   
   RDListIter it = connected_dots.begin( );
   RDListIter ite = connected_dots.end( );

   sorted.push_back( connected_dots[0] );
   RDList skip;
   skip.push_back( connected_dots[0] );
   
   for(; it != ite; ++it ) {
       RoadDot* d = getRight( connected_dots[0] , skip );
       if ( !d ) break;
       skip.push_back( d );
       if ( find( sorted.begin(), sorted.end(), d ) != sorted.end() ) {
           cout << "Double push in sorted!!!" << endl;
       }
       sorted.push_back( d );
   }
   
}

Each time a dot on the right is retrieved, it is added to the skip list for the next search. Sorting, in a word...

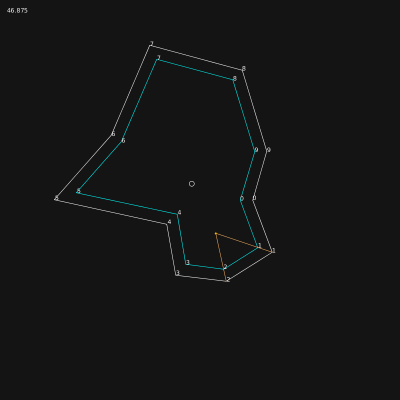
Algorithm can be very painful... but when they are logically correct, they work marvellously! The generation time of each map is nearly unchanged, and results are perfect: no holes!

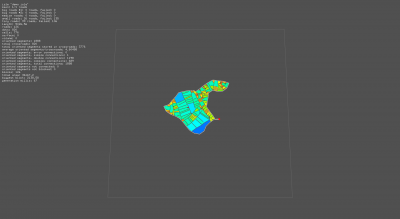
Last screenshot shows the block rendered as plain shapes. The big yellow one is the outer bound of the map! With a method to measure surfaces of a random polygon, I'll be able to have the precise city area.

method

The first implementation of block detection was using the road's segment. The algorithm was starting with the 2 first dots of the first road and was travelling across the network by performing a getRight() at each dot having more than 2 connections.

A --- B ---- C ---- E
             |
             |
             D
A: {B}
B: {B,C}
C: {B,D,E}
E: {C}

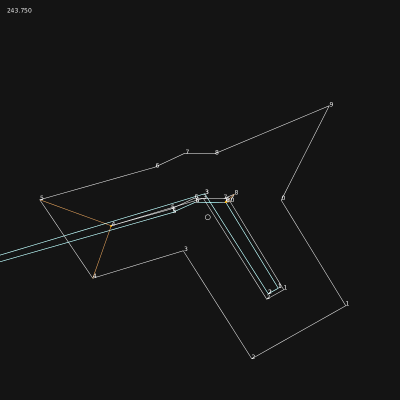
The main issue of this method was that some blocks were not detected! Each time I was passing by through a dot, I was storing wich connections I used. In some cases, the dot needed to be used one time more than its number of connection.

A much better way to perform the search for blocks is based on the half-edges technique. Indeed, each block uses a serie of half-edges, and these half-edges are used only by it. This approach is similar to directed graphs.

Any point of the map is a RoadDot, looking like this:

class RoadDot {
public:
   float x;
   float y;
   float z;
   vector<RoadDot*> connected;

I now using a specialised class for half-edges:

class OrientedSegment {
public:
   RoadDot* from;
   RoadDot* to;
   OrientedSegment* next;

and a class knowing wich half-edges are connected to wich dot:

class CrossRoad {
public:
   vector<OrientedSegment*> arriving; // ending at the key 'roaddot'
   vector<OrientedSegment*> leaving; // starting the key 'roaddot'

The crossroads are stored in a map< RoadDot*, CrossRoad >.

Getting all the half-edges at a given dot is now really easy: you pick the crossroad by looping on dots, and I get 2 lists of half-edges connected to the dot.

The OrientedSegment are generated during roads generation. Once the road's network is built, I run a method to connect all half-edges to each other.

The method is looking like this:

RoadDot* d = (*it); // 'it' is an iterator looping over all roaddots of the network 
CrossRoad& cr = crossroads[d]; // the crossroad list, of type map< RoadDot*, CrossRoad >

if ( d->connected.size( ) == 1 ) {

   cr.arriving[ 0 ]->next = cr.leaving[0];

} else if ( d->connected.size( ) == 2 ) {

   cr.arriving[ 0 ]->next = cr.leaving[1];
   cr.arriving[ 1 ]->next = cr.leaving[0];

} else {

   vector<RoadDot*> sorted_dots;
   d->rightSort( sorted_dots );
   RDListIter first = sorted_dots.begin( );
   RDListIter next = sorted_dots.begin( );
   ++next;
   RDListIter it = sorted_dots.begin( );
   RDListIter last = sorted_dots.end( );
    
   OrientedSegment* os_arriving = 0;
   OrientedSegment* os_leaving = 0;
    
   for (; it != last; ++it, ++next ) {
    
       if ( next == last ) {
           next = first;
       }
    
      os_arriving = cr.getArriving( ( *it ) );
      os_leaving = cr.getLeaving( ( *next ) );
      os_arriving->next = os_leaving;
    
   }
}

After this, all half-edges are connected on each other correctly. Detecting blocks is a ultra-simple:

OrientedSegment* start = os;

Block* b = new Block( );

while ( os->next != start ) {

   b->add( os->from );
   os->blocked = true;
   os = os->next;

}

surfaces

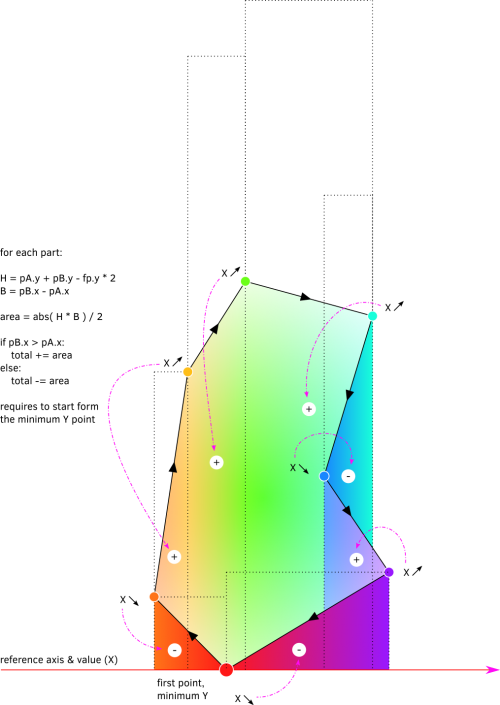
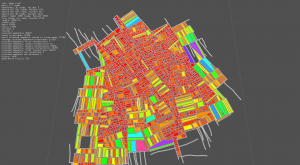
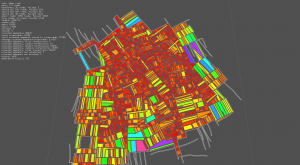
The implementation of the method has been rather quick, even if the results have to be better checked, via a comparaison with a bounding box for instance. The color mapping in the screenshots below is as follow:

• surface ∈ [0,3000]: ( bigger => violet & more grey )
  • hue: [0,3000] → [0,255]
  • saturation [0,3000] → [255,180]
• huge surface (>=3000): white stroke

Image are 1920x1080, click on them to see details.

Legend:

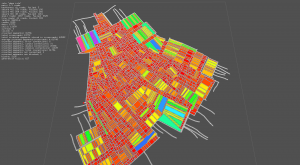
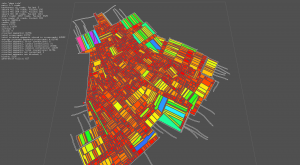
• image #1: block's color depends on surface, roads are displayed as white lines
• image #2: block's color depends on surface, roads are not displayed
• image #3: block outline, a small cross indicates the center of each block

Reviewing surface calculation process > there was an inversion of axis in the computation, and it was missing absolute methods at several places. Surface is validated against the bounding box area. Before corrections, the surface was bigger than the bounding box...

Large and small network.

Fill and stroke of the same map.

Fill and stroke of the same map.

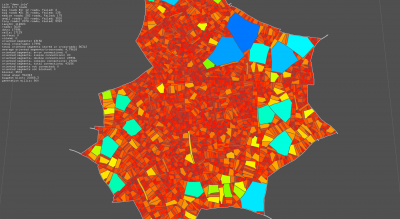
There is a strange cutted edges on a lot of blocks. The block detection must miss a dot in several cases... I hope the bug is not in the half-edges linkage. Must be investigated.

shrinking

After detection, blocks are 'glued' to roads. An offset has to be applied on the shape in order to leave some space for the road itself. The first approach used was to shrink the shape by applying an offset of x along each dot normal. Calculation of the normal is straight forward: perpendicular of the previous segment direction + perpendicular of the next segment direction divided by 2. In pseudo code, it gives:

vec3f previous_dir = (current_dot - previous_dot).cross( UP );
vec3f next_dir = (next_dot - current_dot).cross( UP );
vec3f normal = ( previous_dir.normalised() + next_dir.normalised() ).normalised();

normalised() returns a normalised copy of the vec3f

This approach was not keeping the segment's orientation. The shape was distorted.

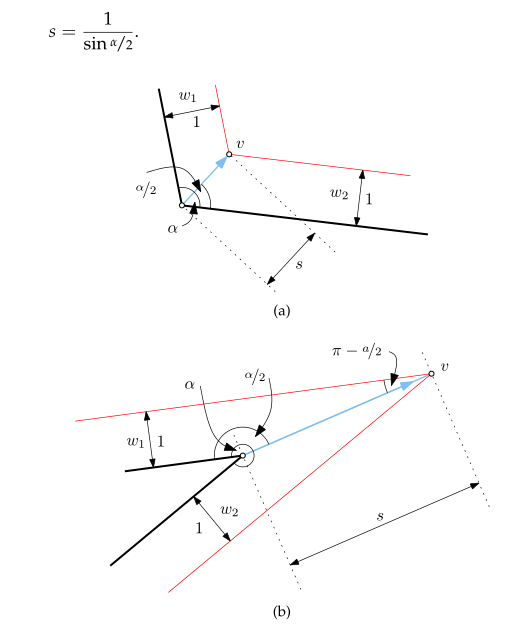
Straight Skeletons

The method of Peter Palfrader called Computing Straight Skeletons by Means of Kinetic Triangulations is proposing a way to solve this y using wavefront propagation.

First step is to move the dots in a way to keep the road segment and the block segment parallel. The math to perform is clearly explained in the thesis, page 14.

Calculation of s, in pseudo-code:

float a = atan2( normale.y, normale.x ) - atan2( previous_dir.y, previous_dir.x );
vec3f shrink_dot = dot + normale * ( 1 / sin( a ) * 0.5 ) * distance;

Java (processing) implementation, with mouse control on the shrinking:

PVector UP = new PVector( 0, 0, 1 );
PVector[] points;
PVector[] normals;
float[] angles;
int num;

void setup() {
 size( 800, 800 );
 num = 10;
 points = new PVector[ num ];
 normals = new PVector[ num ];
 angles = new float[ num ];
 generate();
}

void generate() {
 for ( int i = 0; i < num; ++i ) {
   float a = TWO_PI / num * i;
   float r = random( width * 0.1, width * 0.47 );
   points[ i ] = new PVector( cos(a)*r, sin(a)*r );
 }
 for ( int h = num-1, i = 0, j = 1; i < num; ++h, ++i, ++j ) {
   if ( j >= num ) {
     j = 0;
   }
   if ( h >= num ) {
     h = 0;
   }
   normale( i, points[ h ], points[ i ], points[ j ] );
 }
}

void normale( int i, PVector before, PVector p, PVector after ) {
 PVector dirbefore = new PVector( p.x - before.x, p.y - before.y );
 dirbefore.normalize();
 PVector nbefore = dirbefore.cross( UP );
 nbefore.normalize();
 PVector dirafter = new PVector( after.x - p.x, after.y - p.y );
 dirafter.normalize();
 PVector nafter = dirafter.cross( UP );
 nafter.normalize();
 PVector n = new PVector();
 n.add( nbefore );
 n.add( nafter );
 n.normalize();
 normals[i] = n;
 angles[i] = atan2( n.y, n.x ) - atan2( dirbefore.y, dirbefore.x );
}
void draw() {
 float m = ( ( mouseX * 1.f / width ) - 0.5 ) * width;
 background( 20 );
 pushMatrix();
 translate( width * 0.5, height * 0.5 );
 for ( int h = num-1, i = 0, j = 1; i < num; ++h, ++i, ++j ) {
   if ( j >= num ) {
     j = 0;
   }
   if ( h >= num ) {
     h = 0;
   }
   stroke( 255 );
   line(
     points[ i ].x, points[ i ].y, 
     points[ j ].x, points[ j ].y
     );
   stroke( 0, 255, 0 );
   line(
     points[ i ].x, points[ i ].y, 
     points[ i ].x + normals[i].x * 20, points[ i ].y + normals[i].y * 20
     );
   PVector proi2 = new PVector( 
     points[ i ].x + normals[ i ].x * ( 1 / sin( angles[ i ] ) * 0.5 ) * m, 
     points[ i ].y + normals[ i ].y * ( 1 / sin( angles[ i ] ) * 0.5 ) * m 
     );
   PVector proj2 = new PVector( 
     points[ j ].x + normals[ j ].x * ( 1 / sin( angles[ j ] ) * 0.5 ) * m, 
     points[ j ].y + normals[ j ].y * ( 1 / sin( angles[ j ] ) * 0.5 ) * m 
     );
   stroke( 0, 255, 255 );
   line( proi2.x, proi2.y, proj2.x, proj2.y );
   stroke( 255, 100 );
   line( proi2.x, proi2.y, points[ i ].x, points[ i ].y );
   fill( 255 );
   text( i, proi2.x, proi2.y ); 
 }
 popMatrix();
}

void keyPressed() {
 if ( key == 'g' ) {
   generate();
 } else if ( key == 's' ) {
   save( "straightskeleton_" + year() + "" + month() + "" + day() + "" + hour() + "" + minute() + "" + second() + ".png" );
 }
 println( key );
}

Results are good:

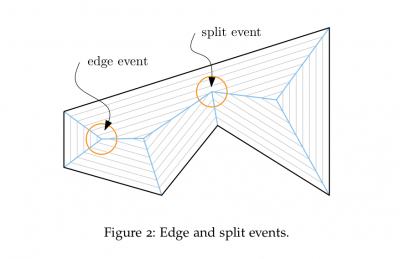
Edge events

The next steps is to locate edges events and split events.

The edges events can be detected easily: the space between 2 points is 0, or the orientation of the shrinked segment is inverted.

Inversion of a vector can be detected like this:

vec2f dir_origin = a¹b¹.normalised();
vec2f dir_shrink = a²b².normalised();
if ( dir_origin.dot( dir_shrink ) < 0 ) {
    // FLIP!
}

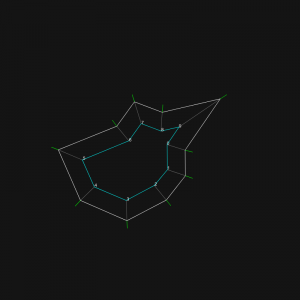
Detection of edges events (called flips in the code).

Approach: a first attempt is performed to shrink the shape at the requested factor. One processed, the generated edges directions are compared to the original shape. If some edges directions are opposite to the originals, I retrieve the intersection between the 2 segments linking the origins to the generated points.

a ------------> b (original segment)
 \             /
   \         /
     \     /
       \ /
        i
       / \
     /     \
    b² <--- a² (generated segment, opposite direction)

A new shape is produce in witch the point a and b are merged, becoming i.

The possible factor for this pass is equals to:

possible_factor = factor * length( a,i ) / length( a, a² )

A new shrink attempt is performed on basis of the new shape, in wich a & b are merged into i, by a factor of orginial_factor - possible_factor.

It's not going too bad, but the process is still very unstable.

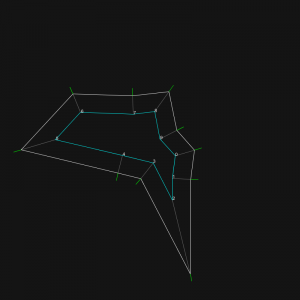
The lack of split events management is provoking this kind of issues:

The point 0 should not be allowed to cross the edge 4,5, and 2 sub polygons should be produced to finish the shrink process.

The method used until now was to try to go to the target factor and check, once applied, if there was issues. If yes, a rollback was performed to the first edge event. A new polygon was generated and a new test performed and so on until the target factor was reached. Shrinking this way causes issues when the shrink factor was far above the maximum (aberrations occur), or the factor between 2 edge events was too small.

In short: trying to go somewhere, hitting a wall on the way and only than seeking a door. It is a bit too stupid to hope the algo will behave in a consistent way...

Edge events are located at the intersection of the dots' normal. Finding them is easy, especially when you already have a method to process intersections of lines and segments . Some of the intersections are pointing toward the center of the shape, others outward. I called this property inner. To render it, I have to verify if the intersection is on the right or left side of the vector.

vec2f cross_point, segment_start, normal_start, segment_end, normal_end;
bool inner;
cross_point = intersection( segment_start, segment_start + normal_start, segment_end, segment_end + normal_end );
inner = ( normal_start.dot( cross_point - segment_start ) < 0 );

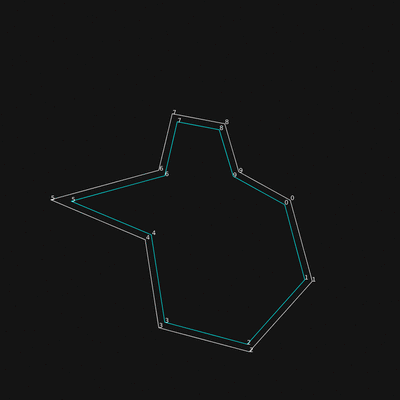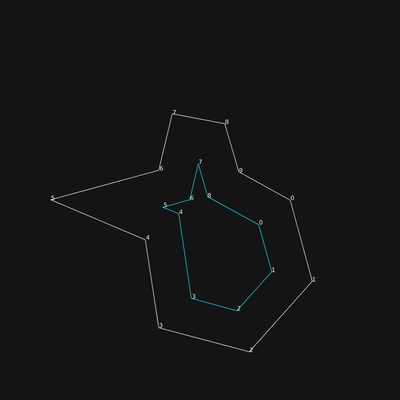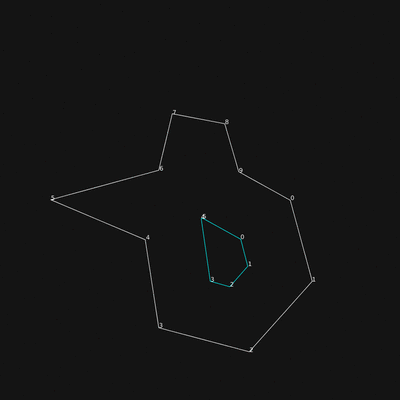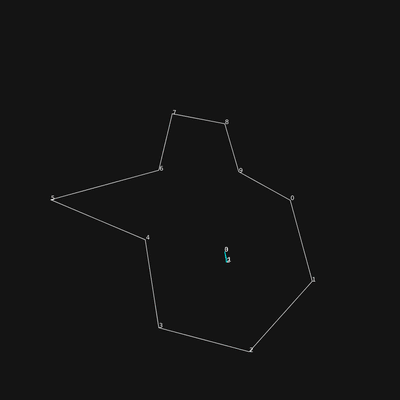
All intersections are detected successfully:

Legend: orange dots are pointing inward, blue ones outward.

Next step is to choose the first intersections that the shrinking shape will meet. The inner marker is very useful in this respect:

• when going outward (negative factor), the blue intersections must be tested;
• when going inward (positive factor), the orange intersections must be tested.

The question of what is the shrinking factor corresponding to this intersection? quickly arouse. We have to inverse the s calculation (see straight skeleton chapter) in this way:

vec2f cross_point, segment_start;
float angle_start;
float intersection_factor = cross_point.dist( segment_start ) /  ( 1 / sin( angle_start ) * 0.5 );

Once done, we just have to pick the smallest intersection factor depending on the factor sign. We can now anticipate the edge events, before making an attempt to shrink.

If shrink factor is less than the smallest intersection factor:

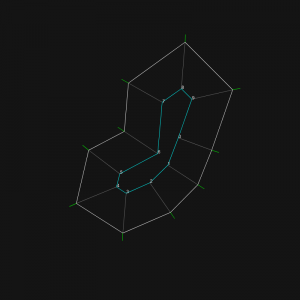
If the shrink factor is high, new polygons are generated on the way, each one containing a reference to the first edge event.

Due to the lack of split event (the next challenge), there are still huge glitches in the process:

Split events

Anticipation of split events requires some brain power.

In the first try, I was computing the intersections between concave angles ( > 180°) and all the segments of the shape. It was nice, in a static shape. But when you shrink a shape, ALL points move, implying that pair point-segment you selected might not be the one where the split event will occur! The prediction was functional, but essentially wrong.

After a cigaret, a full album of the the Mamas & the Papas, some sketches on paper and a sketch on inkscape, a simple solution appeared:

• computing the intersections between concave angles' normal and vector prepared for edge events;
• keeping the intersection where
  • distance to its origin is the smallest and
  • direction is opposite to the normal (to validate).

Colors are inverted in the images below, regarding the color code described in edge events.

The method currently in test is based on intersections between angle bisectors, same approach as the edge events.

During polygon generation, all bisectors are tested on all others, in a separated pass. Bisectors are opposite to the normal vector, this is why you will find - normal in the code below.

Process done at each test:

// finding the intersection between > lines <!
vec2f i = intersection( other.x - other_normal.x, other.y - other_normal.y, current.x - current_normal.x, current.y - current_normal.y );
// verifying that inyersection is inside the shape
if (
   vec2f( i.x - other.x, i.y -  other.y ).cross( other_normal ) > 0 ||
   vec2f( i.x - current.x, i.y -  current.y ).cross( current_normal ) < 0 ||
) {
   // OUTISIDE!
} else {
   // getting the length of the current-intersection segment
   float tmpd = vec2f( i.x - other.x, i.y -  other.y ).length() / abs( 1 / sin( other_angle ) * 0.5 );
   if ( tmpd < current_smallest_dist ) {
      split_pint = i;
   }
}

It is not yet correct: the intersction is inside the shape, ok, but the closest intersection is rarely the good one. Speed is not correctly implemented.

It seems that speed have to be taken into account more seriously. All points move together, meaning that the angle difference between the points influences the crossing time. The more opposite the angles are, the fastest they will cross each other.

Resources

• Doubly connected edge list, also known as half-edge data structure - wikipedia
• Segments' intersection & Segments' crossing in Notes:Math