Difference between revisions of "Conference:HOME CINEMA 3.17"

Revision as of 18:37, 10 April 2017

L’Association Trafic vous convie à l’intervention de l’artiste programmeur François Zajéga. Dans le cadre de cet événement, il traitera directement des rapports entre les arts et le numérique qui font l’objet de notre programmation annuelle en abordant un certain nombre de questions telles que : Quelles sont les implications de la programmation dans la production artistique ? Dans quelle mesure les pièces sont-elles reconfigurées quand elles deviennent des machines ? Comment une démarche artistique s'inscrit-elle dans le code ? À travers une présentation de quelques-unes de ces oeuvres, François Zajéga nous propose une exploration des différentes strates de sa recherche, débutée il y a sept ans. Cette présentation sera l'occasion de synthétiser les relations étroites entre arts, sciences et techniques.

François Zajéga est un artiste programmeur vivant et codant à Bruxelles. Diplômé en infographie et en dessin académique, il s'est formé à la programmation en autodidacte. En 2010, il rejoint l'institut Numédiart de l'Université de Mons, grâce auquel sa production artistique va se teinter de recherche scientifique. Il est aujourd'hui assistant en arts numériques à Arts2, l'école supérieure des arts de Mons. Il travaille actuellement à la création d'objets hybrides, tout aussi inspirés du jeu vidéo que des arts plastiques. Ses oeuvres sont régulièrement présentées en Belgique et en France.

Déroulé

Démo infinite loop en python

i = 1
while( i != 0 ):
    i += 1
    print( i )

Notes

La programmation comme medium.

La nature de l'ordi

Discontinuité

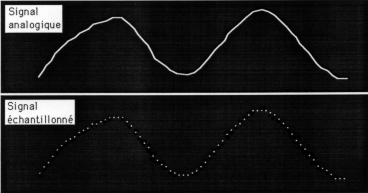
numérique <> analogique

digitalisation, numérisation: segmentation en unités stables temporellement - son

on passe donc de qqle chose de continu (le réel sensible) à une succession d'états, discret.

Binaire

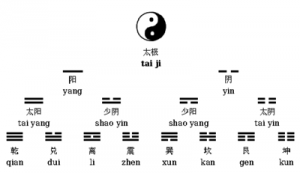
Estimé à 750 av J.C. : traité du Yi Jing ref

Exemple de carte perforée IBM. ref

• Année de création : 1930
• Capacité de stockage : 80 caractères par carte
• Vitesse de lecture : 133 caractères par seconde
• Vitesse d'écriture : 4 caractères à la seconde
• Réécriture possible : non

1950, Vacuum tube logic module from a 700 series IBM computer.

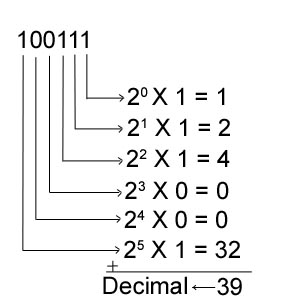
Réduction maximale de la réalité à une succession de VRAI et de FAUX.

Toute information dans une machine informatique est un assemblage de 0 et de 1.

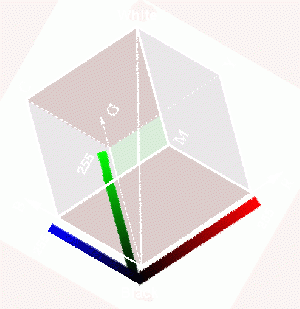
Exemple: couleur sur un écran.

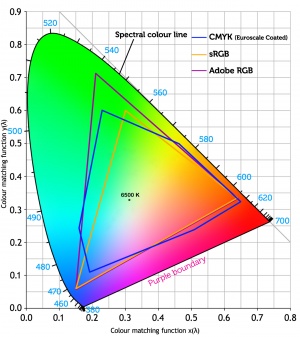
Réduction du spectre:

Réduction à 3 dimensions:

Chaque canal est ensuite tronçonné en 256 valeurs, allant de 0 à 255, sur 8 bits, donc de 00000000 à 11111111

Pour un total de 24 bits, et ce pour chaque pixel d'un écran.

Couleurs perçues par l'humain:

• 000000000000000000000000 >> noir
• 111111110000000000000000 >> rouge
• 000000001111111100000000 >> vert
• 000000000000000011111111 >> bleu
• 111111111111111111111111 >> blanc (luminosité maximum du pixel)

Chaque pixel d'un écran étant constitué de 3 ampoules ayant chacune 256 gradations.

Avec le cinéma digital (ayant une plus grande définition et une plus grande gamme de couleur), l'humain occidental est en permanence exposé à cette réduction.

Turing / Church

Alan Turing - sa machine est avant tout une expérience de pensée. Cette machine sert de base á Thèse de Church qui définit ce qu'est la calculabilité.

Concept fondamental: Fonction calculable -> une opération qui est définie pour toute entrée et qui s'arrête (par là machine de Turing).

Dans une forme dite « physique », elle affirme que la notion physique de la calculabilité, définie comme étant tout traitement systématique réalisable par un processus physique ou mécanique, peut être exprimée par un ensemble de règles de calcul, défini de plusieurs façons dont on a pu démontrer mathématiquement qu'elles sont équivalentes. ref

On connaît de nombreux exemples explicites de fonctions incalculables. Le plus courant est celui du problème de l'arrêt : il n'existe pas de programme universel qui prenne n'importe quel programme en argument et qui, en temps fini, renvoie « oui » si l'exécution du programme reçu en argument finit par s'arrêter et « non » s'il ne finit pas. ref

Un nombre limité de calculs peuvent être opérés à chaque tick d'un processeur. Assurer qu'ils se terminent assure que les suivants peuvent être accomplis. Boucle infinie: la machine semble s'arrêter.

Pour pouvoir être traité par une machine informatique, une question ou une tâche doivent être découpés de cette manière: un ensemble de règles de calcul.

Les règles de calcul dans ce cas sont le jeu d'instructions connu par le CPU (processeur central). Il diffère selon les modèles.

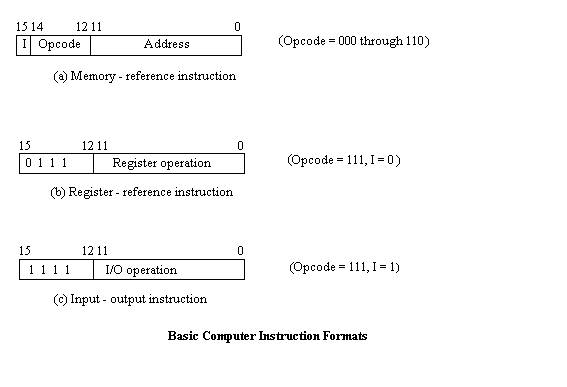
Exemple

Adapted from Figure 5-5, Computer System Architecture, Third Edition by M. Morris Mano, 1993, Prentice Hall.

source: http://people.uncw.edu/tagliarinig/Courses/242/BasicComputer/InstructionFormats.htm

Temps

Zénon d'Élée, paradoxe de la flèche, impossibilité du mouvement.

(problème résolu par la physique quantique)

• Pour pouvoir accomplir une opération, une machine informatique a besoin qu'aucune des opérandes ne se modifie durant l'exécution. ( Concurrent access error ).
• La durée de résolution d'un ensemble d'opérations est variable et est non-instantanée (impliquerait une vitesse infinie). Une série d'opération peut être exécutée facilement (rapide, très rapide voire perçue comme instantanée par un humain) ou au contraire être très difficile à aboutir (sera perçu comme un problème par l'humain). Ex: une balle virtuelle animée par un simulateur physique. Le temps de calcul nécessaire peut varié fortement, brisant du même coup la sensation de continuité >> LAG

Un ensemble d'opérations ~ algorithme.

Un algorithme est une suite finie et non ambiguë d’opérations ou d'instructions permettant de résoudre un problème ou d'obtenir un résultat.

Les ordinateurs sur lesquels s'exécutent ces algorithmes ne sont pas infiniment rapides : le temps de machine reste une ressource limitée, malgré une augmentation constante des performances des ordinateurs. ref

Esprit & corps

Extension de l'esprit cartésien, mathématico-logique. Ne recouvre pas l'entièrté des facultés cognitives humaines!

• Intelligence linguistique
• Intelligence logico-mathématique
• Intelligence spatiale
• Intelligence intra-personnelle
• Intelligence interpersonnelle
• Intelligence corporelle-kinesthésique
• Intelligence musicale
• Intelligence naturaliste (1993)
• Intelligence existentielle (ou spirituelle)

selon a théorie d'Howard Gardner.

Si elle n'était qu'une extension de l'esprit, les machines informatiques resteraient purement théoriques et mentales. Hors, elles sont capables de faire apparaître le résultat de leurs calculs dans le sensible. Un outil capable d'agir sur autre chose que l'esprit devient donc une extension du corps! Manipulations un grand nombre d'interrupteurs de courant électriques.

Processeur i7 quadcore, nombre de transistors: 1,400,000,000 (1 billion 400 millions ), chacun d'une taille de 22 nm ref.

En tant que machine spécialisée dans l'exécution de règles simples en très grand nombre, elle n'a aucune conscience de ce qu'elle traite (voire binaire). Son monde est une succession d'états dans lequels un nombre d'opératons sont à effectuer. Une fois toutes les opérations effectuées, elle s'arrête (la maintenir allumée est une des tâches de l'OS).

.

On peut lui ajouter des mains, des extensions qu'elle contrôle dans son monde, qui est électronique.

Côté machine	Côté sensible

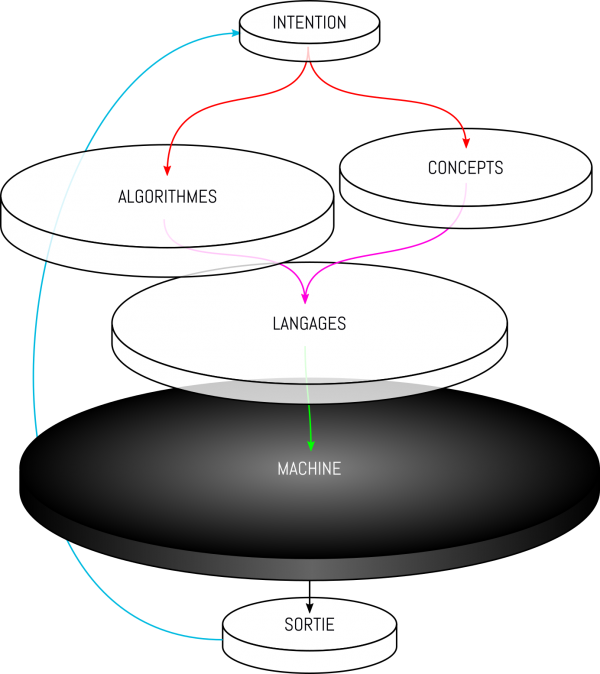
Intention

La force brute des machines informatiques nécessite de formalisé les tâches qui lui sont données à faire. Elles peuvent être complexes tant qu'elle suivent les impératifs de sa nature.

Sol Le Witt, oeuvre sous forme de procédure exécutable par des humains. Permet une très forte condensation des instructions. L'exécutant existe dans le même monde que le concepteur, ils partagent un ensemble de références communes.

Panamarenko - recherche en ingénieurie, ses pièces sont pensées en temps qu'objets fonctionnels ne tenant pas compte des réalités physiques.

Reste donc le problème de l'inscription de l'intention de l'artiste dans le fonctionnement de la machine binaire.

• introduire une intention artistique dans des engrenages -> vision animiste qui voudrait que l'artefact soit dépositaire d'une partie de l'âme de son faiseur (~mythe)
• faire faire à une machine une série d'opérations qui denotent d'une intentionalité perçue comme telle par d'autres humains -> vision matérialiste dans laquelle l'art se trouve non pas dans l'artefact mais dans la psyché. Voir la machine de tinguely.

Il est de la nécessaire de s'approprier les concepts et les languages utilisés par ceux qui ont conçus ces machines: les monde scientifique et technique.

Le concept de beau n'est pas définissable scientifiquement et la philosophie, étant basée sur le language humain, ne peut fournir une définition suffisante et universelle. Il n'est pas possible de le réduire à une successions d'opérations simples.

Il va donc falloir composer avec les outils (modèles) venant de champs non-artistiques et les assembler de telle manière à ce que ce montage puisse être présenté et défendu en tant qu'oeuvre d'art, dénotant de la personnalité de l'artiste.

Pour être protégée par le droit d'auteur, une œuvre doit en premier lieu être originale, c'est-à-dire qu'elle doit porter l'empreinte de la personnalité de son auteur. Ce critère déterminant de l'originalité est éminemment subjectif, ce qui en rend l'appréciation délicate pour les juges en cas de contestation. L'originalité ne doit pas être confondue avec la nouveauté. Ainsi, une création reprenant une idée antérieure peut être originale et bénéficier à ce titre de la protection par le droit d'auteur, comme par exemple une pièce de théâtre sur un thème déjà développé par le passé. [...] Pour bénéficier de la protection juridique du droit d'auteur, il faut que l'idée ait été concrétisée, mise en forme. La protection s'appliquant avant tout à l'expression intellectuelle et artistique, une certaine formalisation rendant ces idées tangibles et matériellement perceptibles est nécessaire. ref

Programmation

Concepts

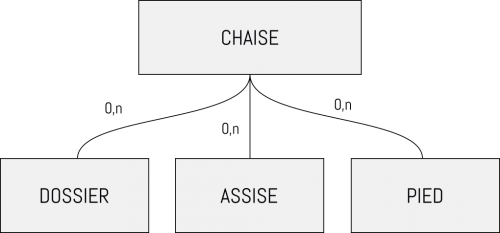
Comment définir une classe (la description d'un objet quelconque en programmation orientée objet). L'idée est de créer une classe permettant de décrire un grand nombre de chaises différentes.

Le modèle chaise

• 1 dossier
• 2 montants pour le dossier
• 1 assise
• 4 pieds

La description de la chaise ne me permet pas de faire des chaises à 1 pieds. Le modèle n'est pas assez flexible (générique) pour e que je veux en faire.

Découpe de la chaise en entités. La chaise cesse d'être une définition rigide pour devenir un ensemble relation entre des éléments autonomes, définis en dehors d'elle.

Cette description est déjà plus souple mais ne pose encore des problèmes:

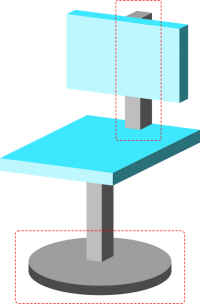
On ne peut pas décrire la forme du pied rond et la montant du dossier. Il va donc falloir retoucher notre modèle.

500px

Le fond diu pied de la chaise à un pied devient une plaque de forme ronde! Les montant peuvent être connectés aux plaques et inversément, la chaise stocke donc maintenant un type d'information supplémentaire: la connextion des éléments entre eux.

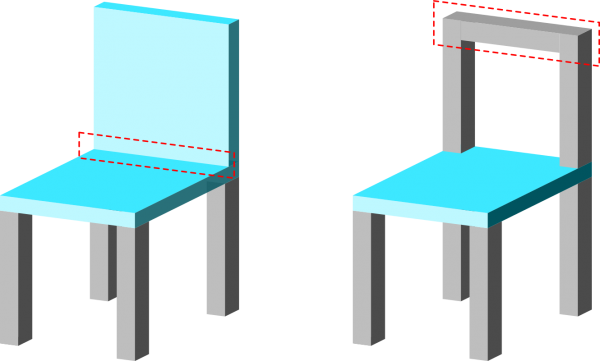
Reste encore des impossibilités dans mon modèle: on ne peut pas connecter 2 montants entre eux, ni deux plaques.

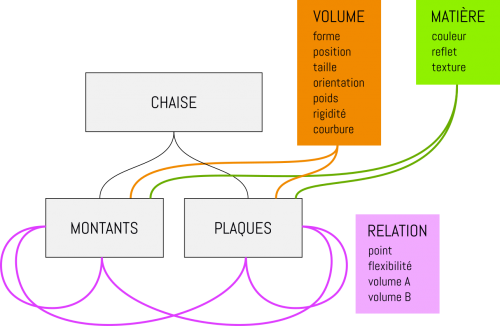
Une fois la relation possible, le modèle devient extrêment flexible et permet de décrire des formes qui n'avaient pas été formalisée mentalement lors de la première ébauche. Il faut maintenant lui injecter des paramètres pour générer des chaises "concrètes".

Un peu plus proche de la réalité:

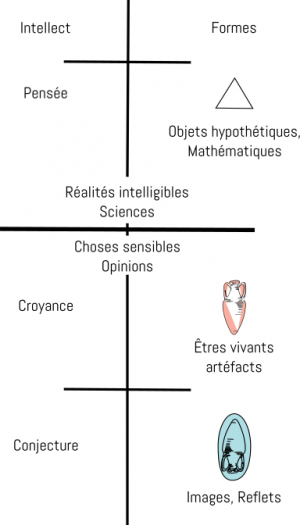
Rapport à la philosophie platonicienne.

Bibliographie

• Ars Industrialis, Réenchanter le monde, La valeur esprit contre le populisme industriel, Bernard Stiegler, Flammarion - Champs essais, 2006 - ISBN 978-2-0812-1784-3
• Le sujet digital édité par Claire Larsonneur, Arnaud Regnauld, Pierre Cassou-Noguès, Sara Touiza, édition presses du réel ISBN 978-2-84066-794-0
• Parole, écriture, code de N. Katherine Hayles, éditions les presses du réel - ISBN 978-2-84066-764-3
• L'art dans le tout numérique de Norbert Hillaire, éditions Manucius - ISBN 978-2-84578-440-6
• Ouvrir le document - Enjeux et pratiques de la documentation dans les arts visuels contemporains de Anne Benichou, éditions Les presses du réel, ISBN 978-2-84066-350-8
• L'artiste, un chercheur pas comme les autres, coordination: F. Renucci et J.-M. Réol, Hermès, La Revue n°72, ISBN 978-2-271-08813-0
• L'Art à l'état gazeux : essai sur le triomphe de l'esthétique, Yves Michaud, Paris, éditions Stock, 2003, ISBN 2-234-05555-5.

Liens

• http://www.hugoverlinde.net/textes/textes.php
• http://blog.illusion-macadam.fr/beau-rencontre-fortuite-table-de-dissection-dune-machine-a-coudre-dun-parapluie-entretien-magali-desbazeille/